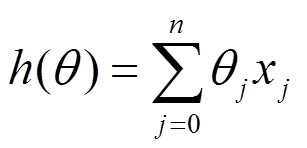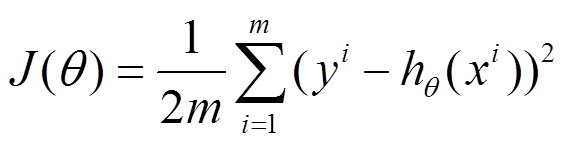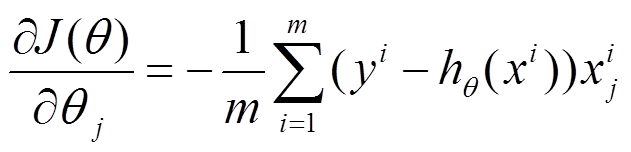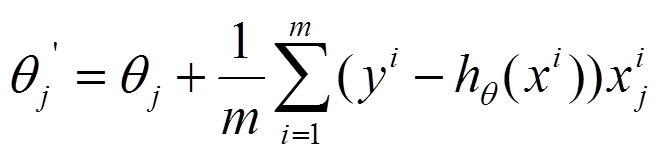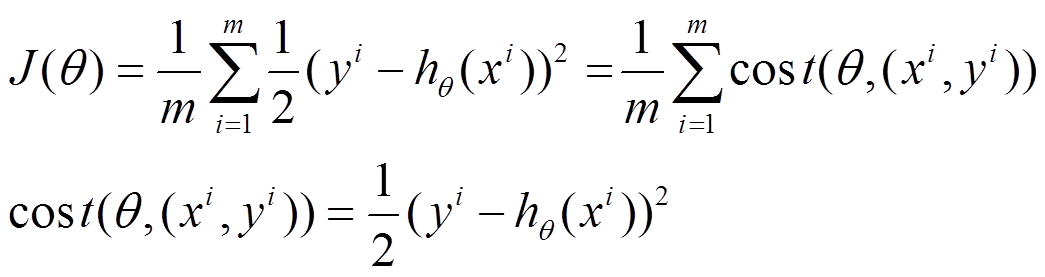转自:

注意下面说的全局最优是特殊的情况，一般还是梯度下降的方法还是很容易变成局部最优。

 

梯度下降（GD）是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种迭代求解思路，下面从公式的角度对两者进行分析。

 

下面的h(x)是要拟合的函数，J(theta)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数，j是参数的个数。

 

1、批量梯度下降的求解思路如下：

（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度

   

（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

 

2、随机梯度下降的求解思路如下：

（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta

（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

 

3、对于上面的linear regression问题，与批量梯度下降对比，随机梯度下降求解的会是最优解吗？

（1）批量梯度下降---最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。

（2）随机梯度下降---最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

 

 

4、梯度下降用来求最优解，哪些问题可以求得全局最优？哪些问题可能局部最优解？

对于上面的linear regression问题，最优化问题对theta的分布是unimodal，即从图形上面看只有一个peak，所以梯度下降最终求得的是全局最优解。然而对于multimodal的问题，因为存在多个peak值，很有可能梯度下降的最终结果是局部最优。